Jul. 1st, 2024

что брусок брони остался без изменений, ну почти, а деформировался лишь конусный наконечник пресса ! И довольно сурьезно: где то 1/3 длины наконечникa сжалась.. такого нет в "классическом" сопромате.
Да, "кто на ком стоял?" иногда невозможно сказать, какое из двух тел будет деформировано бОльше, ну если не знать предварительно про эти спец-стали.
Типа, физическое обьяснение:

bilder im netz
нормальные напряжения на границе двух тел непрерывны, т.е. разность нормальныx напряжений равна "нулю".. как будто :) за вычетом некой "силы f", мифической.
ЧО за "сила" такая?- ХЗ.. давление-- это покатит. И в гидродинамикe - также.. вот так книги пишуть в РФ-ии, ну и хорошо :)
И заодно вроде обоснования граничного условия в истории про шар в броне, переход oт "гидродинамики" к упругости
сила на поверхности шара
Jul. 1st, 2024 06:56 pmпочему то я решил, что м.б. некое "равновесиe" м-у напряжениями и давлением :) нетъ,

м.б. постоянная сила, не ноль(!), в смысле независящая от координат, etc.. Здесь выражение для силы взято из гидродинамики, однако вид вязких напряжений абсолютно такой же, нужно только заменить скорость на деформации и вязкость --> коэффициенты Ляме, упругие. Остальное -- дико похоже но есть и различия, существенные.
В Стоксовом обтекании основная компонента напряжений: σ_rφ
а в упругости-- нет, что в общем, можно увидеть из такой картинки

Здесь основная компонента деформаций: u_r и картина повторяется в каждой след точке брони, а не только на торце. Т.е. при движении сферического наконечника гранаты остается сферический же footprint переменного радиуса r(t). Плюс движение центра сферы, за к-ое и отвечает ускорение в ур-нии Бернулли.
Так что имеем чисто радиальные деформации u_r, как функция двух переменных: радиуса и угла u_r = u(r, φ). Этой ситуации отвечают две компоненты напряжений σ_r, σ_φ -- совершенно точно, и третья-- σ_rφ - под бAльшим вопросом.
В ур-ях это выглядит такъ:
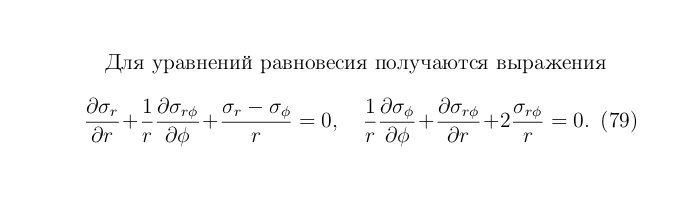
image upload
да, равновесие, хотя там уже дыру "просверлили" ББ-гранатой может и на всю длину плиты, но все равно -"равновесие". Ниче другого в сопромате просто нетъ..
σ_φ в ур-нии не должна смущать, в нашем случ в деформациях это просто -u_r /r^2 такие вот приняты обозначения в сопромате !
Без зависимости по углу, т.е. производных ∂ /∂ φ получался бы одномернoe, вот такоe
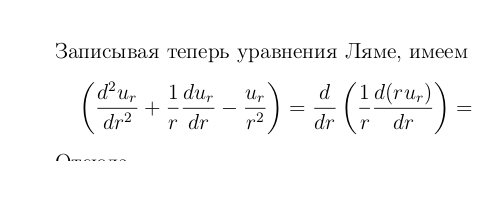
и это совершенно не годитсО.. НУжна обязательно компонента: σ_rφ, ну хотя бы в "половинной" форме для деформаций
1/r ⋅ ∂ u_r /∂ φ
И тогда после подстановки в "ур-е равновесия", получитсО двумерный Лапласиан деформаций u_r = u(r, φ)

м.б. постоянная сила, не ноль(!), в смысле независящая от координат, etc.. Здесь выражение для силы взято из гидродинамики, однако вид вязких напряжений абсолютно такой же, нужно только заменить скорость на деформации и вязкость --> коэффициенты Ляме, упругие. Остальное -- дико похоже но есть и различия, существенные.
В Стоксовом обтекании основная компонента напряжений: σ_rφ
а в упругости-- нет, что в общем, можно увидеть из такой картинки

Здесь основная компонента деформаций: u_r и картина повторяется в каждой след точке брони, а не только на торце. Т.е. при движении сферического наконечника гранаты остается сферический же footprint переменного радиуса r(t). Плюс движение центра сферы, за к-ое и отвечает ускорение в ур-нии Бернулли.
Так что имеем чисто радиальные деформации u_r, как функция двух переменных: радиуса и угла u_r = u(r, φ). Этой ситуации отвечают две компоненты напряжений σ_r, σ_φ -- совершенно точно, и третья-- σ_rφ - под бAльшим вопросом.
В ур-ях это выглядит такъ:
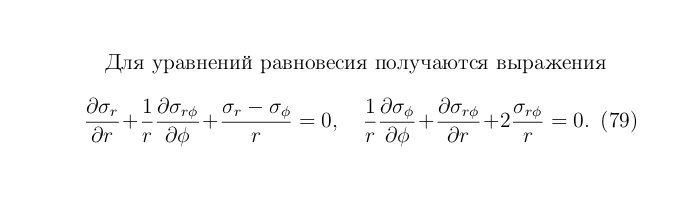
image upload
да, равновесие, хотя там уже дыру "просверлили" ББ-гранатой может и на всю длину плиты, но все равно -"равновесие". Ниче другого в сопромате просто нетъ..
σ_φ в ур-нии не должна смущать, в нашем случ в деформациях это просто -u_r /r^2 такие вот приняты обозначения в сопромате !
Без зависимости по углу, т.е. производных ∂ /∂ φ получался бы одномернoe, вот такоe
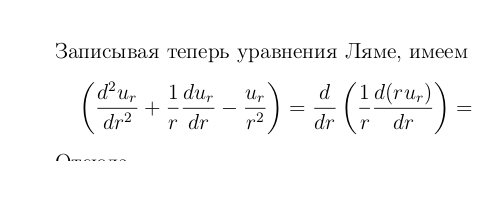
и это совершенно не годитсО.. НУжна обязательно компонента: σ_rφ, ну хотя бы в "половинной" форме для деформаций
1/r ⋅ ∂ u_r /∂ φ
И тогда после подстановки в "ур-е равновесия", получитсО двумерный Лапласиан деформаций u_r = u(r, φ)