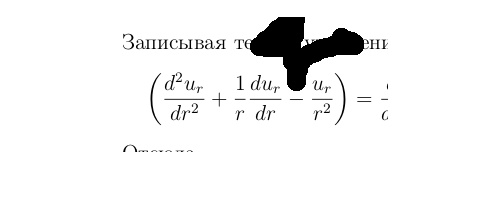(no subject)

https://www.youtube.com/watch?v=M0MWa2NdmPk
Smoothest Impact Crater Simulation
из той же серии "тупизны", пригодитсО..

https://www.youtube.com/watch?v=ztQ8l5r__Ik

как сэкономить время при решении диффуров?

оч просто, нужно открыть Ландау и внимательно посмотреть, как правильно записывается сила, действующая на тело в жидкости, в тензорных обозначениях:

да, поскольку n --вектор, направленный по нормали к поверхности шара, вдоль радиуса, будут лишь две компоненты тензора напряжений: σ_r и σ_rφ
И никаких там σ_φ для шара, движущегося в броне. В сопромате то нет движения, сАвсем.

Речь о вот этом диффуре, Лапласо--"подобном"

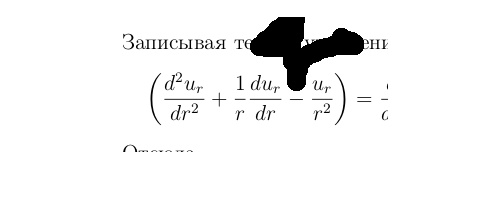
в последнем слагаемом "- 4u/r^2" для двойного угла: u = u(r) cos2θ

Альтернативный взгляд, что есть все три компоненты напряжений, просто в силу входят только две.. Да, вот так пожалуй будет верно ! Иначе непонятно, почему это u_r / r^2 д.б. равно нулю вблизи шара?
Так что, да все равно нужно решать бигармоническое, иначе будут "странные" слагаемые вроде "- 5u/r^2" или "- 2u/r^2"в Лапласе.