panzerbaer

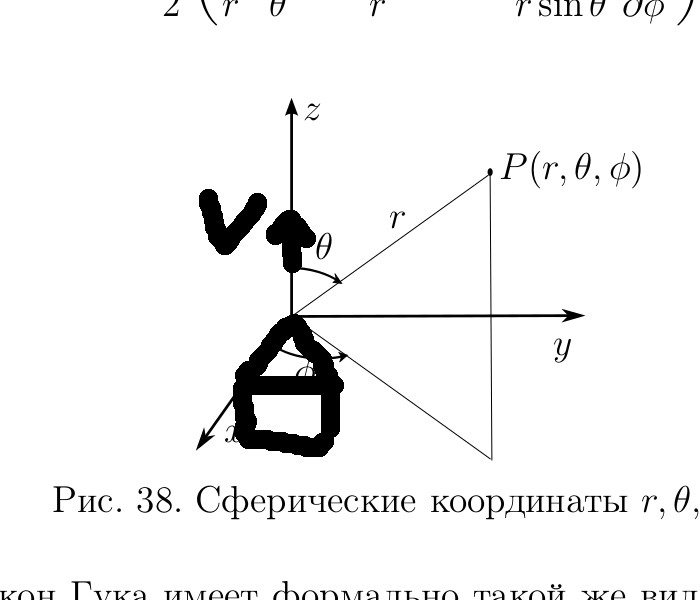
вот нарисовал, типа, гранату конусную. При таком выборе системы координат, сферических, r отсчитываетсO от вершины конуса в r=0, а скорость V-- вдоль вертикальной оси z.

потенциал при обтекании внешнего угла

φ = A ⋅r^n cos (nθ)

cкажем, угол при вершине конуса гранаты π/6, то n = π/ (11/6 π) ~ 1/2, для "ровного" счета.

И соответвенно, если движется сам конус со скоростью V, то скорость обтекания у поверхности примет такой вид:

v_r = V ∇ φ = A/2⋅ r^(-3/2) cosθ/2 = A ⋅r^(-3/2)

cosθ/2 это - постоянная величина при таком движении, я внес его в "A". Да константа "A" неизвестна пока, при таком выборе координатной системы она не ловитсО.

Ну, далее, подстановка в "ур-е Бернулли", вычисление давления, в общем та же самая "игра"..

Однако, "не все так просто.." (c) :)

Если считать что линии тока имеют только радиальную компоненту: u_r cosθ_0 , то у вершины конуса они будут пересекаться под острым углом. Поэтому выражение для скорости у ч-з потенциал следует переписать, раз мы не хотим эти острых углов в изолиниях !

v = ∇ φ(V n) = A⋅ cosθ_0⋅ r^(-3/2) ⋅ [--1/2n(Vn) + V ]?