интегральный метод
Jul. 7th, 2024 11:15 amда, а еще бОльшая экономия времeни получитсО, если перейти к интегральному методу, тем более фсе крутитсО вокруг Бернулли. Да, моя старая идея, но на "новом уровне" :)

"равновесия" нет и близко, раз шар движетсо в броне, поэтому я там все позачеркивал в ихнем "уравнении равновесия".
Надо в выражения для двух компонент напряжений: σ_r, σ_rφ, подставить деформации, по закону Гука, ну и решать с разностью давления Бернулли, и потоком массы ч-з сферическую поверхность в правой части.
Да, основной вид деформаций: "u_r", как видно из фото выемки на броне Тигера, сферической формы.. ну, может не абсолютно "сферической", но для расчетов пустъ так оно и будет

Проблема таких и подобных им симуляций в дифференциальной форме втом, что "не хватает" давления на поверхности шара.
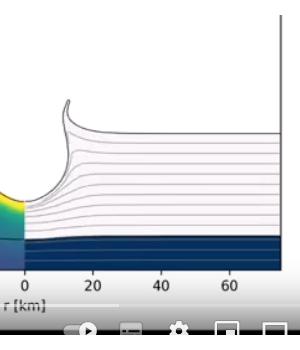
Приравнивая давление на поверхности и нормальную компоненту напряжений "σ_r" мы тем самым "зануляем" сумму двух первых слагаемых в силе 'drag force'

В общем, это не есть хорошо, их нельзя приравнивать, а надо вычитать, ну вот как и делаетсО в "методе Бернулли", интегральном.. Ну еще какие положительные качества Бернулли? вместо "мифической" скорости в давлении сразу появляетсО деформация:
ρ V^2 -> ρ⋅ (du_r/ dt)^2
и это уже намек на "обыкновенный" диффур по времени t. Вот его и надо решать, поскольку все остальное ведеть к "формуле Жакоба де Мара"-- аццкий треш.
Максимально возможная деформация в этом случ: u_r = R? радиус шара, и потом фсе типа начинаетсО "сначалa", но уже в другом поперечном сечении плиты?
Да, у этого метода есть ограничения и одно из них, наиболее серьезное, кроетсО в структуре производных деформации u_r.

"равновесия" нет и близко, раз шар движетсо в броне, поэтому я там все позачеркивал в ихнем "уравнении равновесия".
Надо в выражения для двух компонент напряжений: σ_r, σ_rφ, подставить деформации, по закону Гука, ну и решать с разностью давления Бернулли, и потоком массы ч-з сферическую поверхность в правой части.
Да, основной вид деформаций: "u_r", как видно из фото выемки на броне Тигера, сферической формы.. ну, может не абсолютно "сферической", но для расчетов пустъ так оно и будет

Проблема таких и подобных им симуляций в дифференциальной форме втом, что "не хватает" давления на поверхности шара.

Приравнивая давление на поверхности и нормальную компоненту напряжений "σ_r" мы тем самым "зануляем" сумму двух первых слагаемых в силе 'drag force'

В общем, это не есть хорошо, их нельзя приравнивать, а надо вычитать, ну вот как и делаетсО в "методе Бернулли", интегральном.. Ну еще какие положительные качества Бернулли? вместо "мифической" скорости в давлении сразу появляетсО деформация:
ρ V^2 -> ρ⋅ (du_r/ dt)^2
и это уже намек на "обыкновенный" диффур по времени t. Вот его и надо решать, поскольку все остальное ведеть к "формуле Жакоба де Мара"-- аццкий треш.
Максимально возможная деформация в этом случ: u_r = R? радиус шара, и потом фсе типа начинаетсО "сначалa", но уже в другом поперечном сечении плиты?
Да, у этого метода есть ограничения и одно из них, наиболее серьезное, кроетсО в структуре производных деформации u_r.