![[personal profile]](https://www.dreamwidth.org/img/silk/identity/user.png){kind=small}
panzerbaerда, похоже, удалось "хакнуть" это дело !
много чЕталпЭйсбоок, слушал Manu Chao, но, в общем то, ответ лежал на поверхности:
upload images
из Зельдовича довоольно пространный отрывок про движение газа в 'центрально--симметричном' случае..
Ну т.е. газ движетсО в неком направлении со скоростью "w" и фсе параметры зависят лишь от времени и радиуса r.. Да, ур-ние сохранения массы, или "непрерывности", последнее в тексте, из которого следует, что нек-я величина, "поток", сохраняется при движении шара ч-з броне-плиту:
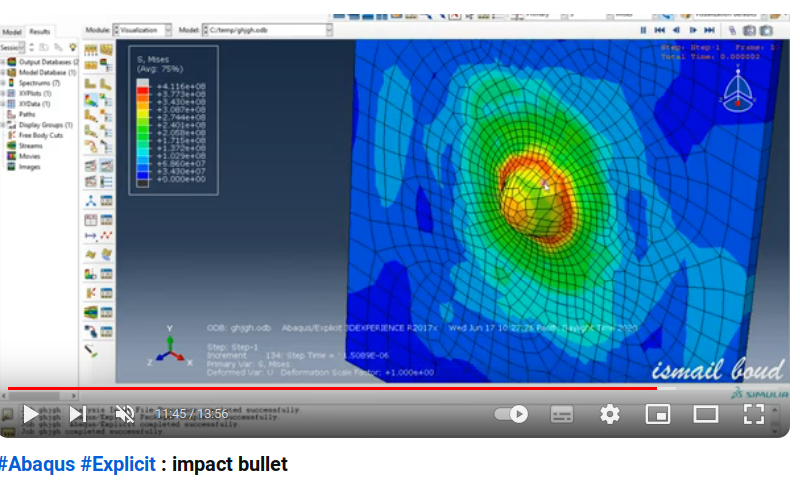
в упругости нет изменения плотности вещества, а есть только изменения объема, так что "∂ ρ/∂t" в его уравнении равно нулю в случае шара в броне. СохраняетсО вот такая величина, "поток массы" постоянный:
r^2 w = R^2(t) dR/dt = const
r- радиус отсчитывается от поверхности плиты. И это соотношение выполняется для любого поперечного сечения в объеме слитка, ну поскольку масса гранаты неизменна. Однако в таком случ, и радис и скорость шара менялись бы по времени вот по закону "zick--zack", пило-образному:
ну.. так скорость гранаты в плите совершенно точно не может менятсО, поэтому возникает некий "парадокс" !
И чтобы его устранить, нужно допустить, что скорость шара везде "постоянна", ну кроме первой и последней поверхности плиты. Только так и можно удовлетворить фсем противоречивым условиям, вот так математически это выглядит
σ_r(R) + ρ V^2 = ρ1 R^2⋅ V = [ 4A R^3 -A b^2 R -2A b^6 / R^3 ] λ + ρ V^2
т.е. квадратное уравнение для скорости шара 'V', да, с учетом плотностей среды ρ и гранаты ρ1.
Потому то в "формуле Жакоба",нашего де Марра, стоит дробная степень в калибре гранаты d^(.7) для "критической скорости" гранаты
и ффсесxодитсО !! Нетъ, не сxодитсО, поскольку по формуле корней квадратного ур-я для "критической" скорости:
V_c = [ (ρ1 R^2)^2 - ρ⋅ 4AR^3 λ] ^(1/2);;;;;;;;;;;;;; V_c ~ R^3/2
можно конечно и так записать: V_c ~ (b^2 R) ^1/2 , но неV_c ~ R^(.7) !
Более современные представления "критической" скорости
это из статейки советского времени, по-моему, шаг назад, по сравнению с "формулой де Марра" :)). Ну во первых, в упругости нет "твердости динамической", в сопромате--есть, но это - техническая наука, и она "сAсет".. после тензорной алгебры, "задач Ламе" и проч.
Во вторых, они просто приравняли напряжения на поверхности гранаты и V-квадрат: "σ(R) = k ρ V^2";
а поток массы "шара" где у них?-- нетути..
Вот такие смешные "улучшения" классики, приСталЕне де Марре такой хуйни не было !
много чЕтал
upload images
из Зельдовича довоольно пространный отрывок про движение газа в 'центрально--симметричном' случае..
Ну т.е. газ движетсО в неком направлении со скоростью "w" и фсе параметры зависят лишь от времени и радиуса r.. Да, ур-ние сохранения массы, или "непрерывности", последнее в тексте, из которого следует, что нек-я величина, "поток", сохраняется при движении шара ч-з броне-плиту:
в упругости нет изменения плотности вещества, а есть только изменения объема, так что "∂ ρ/∂t" в его уравнении равно нулю в случае шара в броне. СохраняетсО вот такая величина, "поток массы" постоянный:
r^2 w = R^2(t) dR/dt = const
r- радиус отсчитывается от поверхности плиты. И это соотношение выполняется для любого поперечного сечения в объеме слитка, ну поскольку масса гранаты неизменна. Однако в таком случ, и радис и скорость шара менялись бы по времени вот по закону "zick--zack", пило-образному:
ну.. так скорость гранаты в плите совершенно точно не может менятсО, поэтому возникает некий "парадокс" !
И чтобы его устранить, нужно допустить, что скорость шара везде "постоянна", ну кроме первой и последней поверхности плиты. Только так и можно удовлетворить фсем противоречивым условиям, вот так математически это выглядит
σ_r(R) + ρ V^2 = ρ1 R^2⋅ V = [ 4A R^3 -A b^2 R -2A b^6 / R^3 ] λ + ρ V^2
т.е. квадратное уравнение для скорости шара 'V', да, с учетом плотностей среды ρ и гранаты ρ1.
Потому то в "формуле Жакоба",
и ффсе
V_c = [ (ρ1 R^2)^2 - ρ⋅ 4AR^3 λ] ^(1/2);;;;;;;;;;;;;; V_c ~ R^3/2
можно конечно и так записать: V_c ~ (b^2 R) ^1/2 , но не
Более современные представления "критической" скорости
это из статейки советского времени, по-моему, шаг назад, по сравнению с "формулой де Марра" :)). Ну во первых, в упругости нет "твердости динамической", в сопромате--есть, но это - техническая наука, и она "сAсет".. после тензорной алгебры, "задач Ламе" и проч.
Во вторых, они просто приравняли напряжения на поверхности гранаты и V-квадрат: "σ(R) = k ρ V^2";
а поток массы "шара" где у них?-- нетути..
Вот такие смешные "улучшения" классики, при
