![[personal profile]](https://www.dreamwidth.org/img/silk/identity/user.png){kind=small}
panzerbaerслова из бессмертного фильма "Хождения по мукам" вполне подойдут.. для описания подкалиберного в броне/ APFSDS ! Где то вот этот отрывок, хотя я не нашел там эту ремарку Теплова, кажись..
https://www.youtube.com/watch?v=OMk27V3LlcE&t=81s
А кроме того,Корнилов Неженцев: "трех-дюймовые, пушечные-- то что надо", тоже бессмертное. Ну я думаю, авторы фильма в гробу бы перевернулись, узнай они такое :)
Да, так вот, "волны" в подкалиберном, что это такое? И да и нет: оч условные "волны", однако же, этим пользуются на практике, ну скажем, считается, что при проникновении подкалиберного в броне-плиту возникает также и ударная волнa, слабая.. При этом просто обязаны быть и колебания плотности деформируемого металла, оч небольшие, но все же. И это один из центральных пунктов теории т. Зельдовича, что в газах, что в твердом.
Сразу же фиксируем противоречие с теорией упругости, там нет изменения плотности по времени, вообще, насколько я знаю, а есть только изменения объема. Такие вот "кошки--мышки", "виляИтЬ..", т.ч. без математики-- никудa не детсО..
Если немного порисовать, ситуация выглядит такъ:
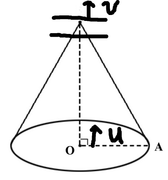
при ударе заостренного наконечника возникают деформации в подкалиберном, да, деформационная "волна" 'u'. Она же проходит спокойно и далее по броне, высокой плотности, что я и нарисовал. Ну конечно не "плоская" волна, как у меня, a скорее со сферическим фронтом, но это --детали, всякие..
Cкорость движения наконечника в броне "v" -это и есть "поршень Зельдовича". И есть возмущения, движущиеся со скоростью звука в металле, "D", ну пусть будет как у него. М-у "D" и "v" есть связь, т.е. уравнение, вроде как и у него, но это-- todo..
Математические такие "волны" описываются ур-ем, типа Гельмгольца, ч-з упругие постоянные Ляме
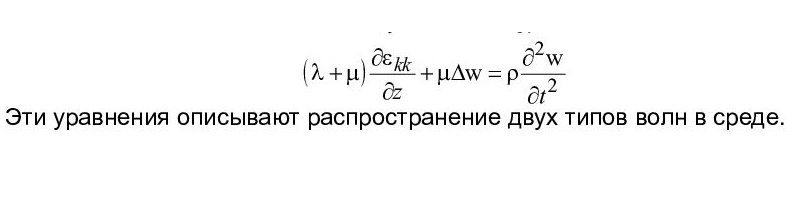
я оставил лишь одну компоненту деформаций, ну как-будто у нас чисто "продолНые волны", т.е. деформации лежат "в плоскости" волнового вектора k.
Да "бегущая волна", как нетрудно заметить, и это решаетсО, но есть одно "НО"-- она сверхзвуковая. Hужны колебания плотности ρ в металле. Ну в общем, аддский "заколдованный круг" выходит, a как его "разорвать"? математикой.. ога!
Да, запись будет продолжена по тегу "пластические деформации", не писать же мне тексты где то в Ворде/дриме/notepad..
https://www.youtube.com/watch?v=OMk27V3LlcE&t=81s
А кроме того,
Да, так вот, "волны" в подкалиберном, что это такое? И да и нет: оч условные "волны", однако же, этим пользуются на практике, ну скажем, считается, что при проникновении подкалиберного в броне-плиту возникает также и ударная волнa, слабая.. При этом просто обязаны быть и колебания плотности деформируемого металла, оч небольшие, но все же. И это один из центральных пунктов теории т. Зельдовича, что в газах, что в твердом.
Сразу же фиксируем противоречие с теорией упругости, там нет изменения плотности по времени, вообще, насколько я знаю, а есть только изменения объема. Такие вот "кошки--мышки", "виляИтЬ..", т.ч. без математики-- никудa не детсО..
Если немного порисовать, ситуация выглядит такъ:
при ударе заостренного наконечника возникают деформации в подкалиберном, да, деформационная "волна" 'u'. Она же проходит спокойно и далее по броне, высокой плотности, что я и нарисовал. Ну конечно не "плоская" волна, как у меня, a скорее со сферическим фронтом, но это --детали, всякие..
Cкорость движения наконечника в броне "v" -это и есть "поршень Зельдовича". И есть возмущения, движущиеся со скоростью звука в металле, "D", ну пусть будет как у него. М-у "D" и "v" есть связь, т.е. уравнение, вроде как и у него, но это-- todo..
Математические такие "волны" описываются ур-ем, типа Гельмгольца, ч-з упругие постоянные Ляме
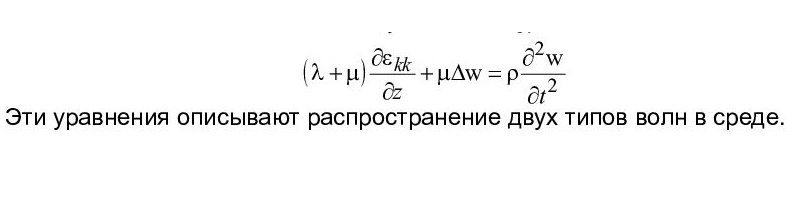
я оставил лишь одну компоненту деформаций, ну как-будто у нас чисто "продолНые волны", т.е. деформации лежат "в плоскости" волнового вектора k.
Да "бегущая волна", как нетрудно заметить, и это решаетсО, но есть одно "НО"-- она сверхзвуковая. Hужны колебания плотности ρ в металле. Ну в общем, аддский "заколдованный круг" выходит, a как его "разорвать"? математикой.. ога!
Да, запись будет продолжена по тегу "пластические деформации", не писать же мне тексты где то в Ворде/дриме/notepad..
